Although the set of notes you have requested is presented below, it has not been maintained since January, 2003. All of the information in these notes has been included in an on-line text titled Computer Organization and Design Fundamentals. The book is available in three formats, two of which are free electronic downloads. Please visit one of the following links in order to access the format you prefer.
Thank you for your interest in this textbook. Please feel free to e-mail me at tarnoff etsu.edu if you have any questions or comments.
-Dave Tarnoff
Reading: Floyd, Sections 2.4 through 2.6
In order to better understand the operation of the processor, it is helpful to learn the basics of binary arithmetic.
As we discussed last period, an analogy can be drawn between decimal counting and binary counting. Binary addition is also analogous to decimal addition, the difference being that decimal has 10 numerals while binary has 2. In decimal, when there is an "overflow" or "carry" due to the result of the addition of two digits being greater than 9, a one is carried to the next position. Similarly for binary, an overflow caused by adding 1 and 1 has a result of 0 and a carry of 1.
|
|
|
|
The last addition 12 + 12 = 102 is equivalent to the decimal addition 110 + 110 = 210. Review last week's notes to see how the conversion of 102 gives us 210.
But how often does decimal addition take the form of a single digit plus a single digit? Not very often. Usually, there are digits in the ten's, hundred's, thousand's, or higher columns. Similarly binary addition is rarely the addition of one binary digit to another. Therefore, we need to know how to handle the carry so that it can be added to the next most significant it.
In decimal, wham a carry occurs, it adds a one to be added to the next highest column. This means that three digits are to be added together: the carried one from the previous column and the original two digits in the column.
In binary, handling the carry adds four more cases to the four possible additions above. The additions below show the results when a carry is added. (Note that the highlighted digits are carries to add to the next most significant digit.)
|
|
|
|
|
Now let's try to add numbers with multiple digits. The example below shows the addition of 10010110 and 00101011. Once again, the highlighted values are the carries from the previous column's addition, and just as in decimal addition, they are added to the next most significant digit/bit.
1 1 1 1 1 |
1 0 0 1 0 1 1 0 |
+ 0 0 1 0 1 0 1 1 |
1 1 0 0 0 0 0 1 |
Once again, we're going to use the analogy with the decimal operation. Starting with the subtraction of single digits, it's fairly straightforward when the value being subtracted from (the minuend) is greater than the value subtracting from it (the subtrahend).
|
|
|
|
But what happens in the case when the minuend is less than the subtrahend? Well, as in decimal, a borrow must occur from the next most significant digit.
In decimal, this would be equivalent to 2 - 1 = 1.
Now let's see how this works with a multi-bit example.
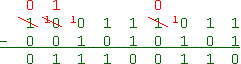
Starting at the rightmost bit, 1 subtracts from 1 to give us zero. In the next column, 0 subtracts from 1 resulting in 1. We're okay so far with no borrows required. The next column representing the 22 digit, however, subtracts 1 from 0. Therefore we need to borrow from the next highest digit.
The next highest digit is a 1, so we subtract 1 from it and add 10 to the digit in the 22 column. This makes our subtraction 10 - 1 which equals 1. Now we go to the 23 column. After the borrow, we have 0 - 0 which equals 0.
We need to make a borrow again in the third column from the left, but the second column from the left is zero and does not have anything to borrow. Therefore, the next highest digit is borrowed from. The borrow is cascaded down until it reaches the third column so that the subtraction may be performed.
Due to factors to be examined later in the course, multiplication and division is a time-intensive operation for processors. Therefore, programmers use a trick to divide or multiply by powers of two in binary.
Examine the table below to see if you can see a pattern in the multiples of two of the binary number 1001.
| Decimal | Binary | ||||||||
| 9 | 1 | 0 | 0 | 1 | |||||
| 18 | 1 | 0 | 0 | 1 | 0 | ||||
| 36 | 1 | 0 | 0 | 1 | 0 | 0 | |||
| 72 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | ||
| 144 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 288 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
Note that to multiply by two, a simple shift of all the bits one position to the left accomplishes this. Similarly, a division by two is accomplished by a right shift one position. This is one way to quickly perform a multiplication or division when the is a power of 2. Simply left or right shift the original value by the number of bits equal to the power. For example, a division by 24 is equivalent to a right shift by 4 bit positions.
Note that if the bits shifted out of the right-most bit (least significant bit) are discarded, this is similar to integer division where the remainders are discarded.
In decimal arithmetic, every number has an additive complement, i.e., a value that can be added to the original number that forces a result of zero. For example, 5 and -5 are additive complements because 5 + (-5) = 0.
This section describes the method for calculating the complements of binary values.
The one's complement simply inverts each bit of a binary value, substituting 1's for all of the 0's and 0's for all of the 1's. An example is shown below.
| Previous value | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1's complement | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
The 1's complement of a value is useful for some types of digital functions, but completely useless for arithmetic. See what happens when we add a value to its 1's complement.
1 0 0 1 0 1 1 0 |
+ 0 1 1 0 1 0 0 1 |
1 1 1 1 1 1 1 1 |
If the two values were additive complements, the result should be zero, right? Well, that takes us to the 2's complement.
Examination of the previous value shows that if we add 1 to the resulting 111111112, then we get a result of 000000002 with an overflow carry of 1. Using this information, we come up with a complement called the 2's complement.
The 2's complement of a value is found by first taking the 1's complement, then incrementing the result by 1. For example, in the previous section, we determined that the 1's complement of 100101112 is 011010002. If we add 1 to this value, we get:
0 1 1 0 1 0 0 0 |
+ 1 |
0 1 1 0 1 0 0 1 |
Therefore, the 2's complement of 100101112 is 011010012. Let's see what happens when we try to add the value to it's two's complement.
1 1 1 1 1 1 1 1 |
1 0 0 1 0 1 1 1 |
+ 0 1 1 0 1 0 0 1 |
0 0 0 0 0 0 0 0 |
The result is zero! Okay, so most of you caught the fact that I didn't drop down the last carry which would've made the result 1000000002. This is not a problem, because the carry was what we call an overflow. As long as we keep track of the number of bits that we started with, then any bits that go past that should be discarded. Actually, discarded is not quite the right term. It should be remembered in case we need to use it later to evaluate the types of numbers that were just added, but it should not be included in the result of the addition. (This is simply the first of many "anomalies" that must be watched when working with a limited number of bits.)
Two more examples of 2's complements are shown below.
| Original value | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1's complement | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 2's complement | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| Original value | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1's complement | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 2's complement | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
There is also a "short-cut" to calculating the 2's complement of a binary number. This trick can be used if you find the previous way too cumbersome or if you'd like a way to verify your answer.
The trick works by copying down the bits starting with the right-most bit until you reach your first binary 1. Copy that 1 down too, then invert all of the remaining bits. This description doesn't make sense to you? Well, look at the example below to see if that helps.
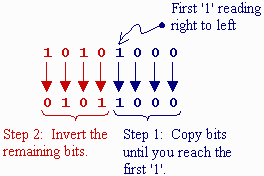
This result matches the result we arrived at for the previous example.
In decimal, the negative of 5 is -5. In addition, the negative of -5 is 5. In other words, taking the negative of a value toggles it back and forth between two values. The same is true for taking the 2's complement of a binary number. For example, the binary value for the decimal value 45 is 001011012. Watch what happens when we take the 2's complement twice.
| Original value = 45 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1's complement of 45 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 2's complement of 45 = -45 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1's complement of -45 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 2's complement of -45 = 45 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
It worked! The second time the complement was taken, the pattern of ones and zeros returned to the original form.
There is one more thing to note. As was stated earlier, 2's complement is used to allow the computer to represent the additive complement of a binary number, i.e., negative numbers. Is there a way for us to tell which value, the positive or the negative, that a binary number represents? Of course there is.
From the earlier description of the 2's complement short-cut, you can see that except for the special cases where the binary value is all zeros or only the MSB is set to a 1, the MSB of the 2's complement is always the inverse of the original value. In other words, except for the two special cases, when we apply the shortcut we will always encounter a 1 before we get to the MSB when reading right to left. And since every bit after this one will be inverted, then the MSB will have to be inverted toggling it from its original value. Therefore, one of the values has a one in the MSB while its 2's complement has a zero. Because of this trait of the 2's complement, the MSB of a value can be used to indicate whether a number is positive or negative.
This also reveals another thing. Since the MSB is being used to indicate the sign, it cannot be used to represent a power of 2, i.e., if a number is said to represent a 2's complement value, only n-1 of its n bits can be used for powers of 2 while the MSB is used for the sign.
Oh, and just to let you know which value is represented by the MSB, binary values with a 0 as the MSB are positive and binary values with a 1 as the MSB are negative.
A less useful way to represent positive and negative binary numbers is to simply take the MSB and use it as a sign bit much like a plus or minus sign and leave the remaining bits to represent the magnitude. For example, -45 and +45 would be identical in binary except for the MSB which would be set to a 1 for -45 and a 0 for +45 as is shown in the table below for an 8 bit representation.
| +45 in binary | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| -4510 using signed magnitude | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
The sign bit (which has no effect on the magnitude) is the MSB highlighted in the table above.
Since the MSB plays an important roll in the representation of the sign of a binary value, it is vital that we know how many bits a particular number is being represented with so we know exactly where the MSB is. In other words, the leading zeros of a binary value may have been removed making it look like the binary value is negative since it starts with a one. For example, the binary value 100101002 means one thing as an 8 bit number and a different thing as a 10 bit number.
100101002 Represented With 8 Bits is a Negative Number
| Meaning of bit position | sign | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Binary value | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
100101002 Represented With 10 Bits is a Positive Number
| Meaning of bit position | sign | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Binary value | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
Since computers don't use an infinite number of bits to represent values, software must know two things before it can interpret a binary value: the number of bits and the type of binary representation. This usually is confusing for the novice. It means that the 8 bit number 101001102 represents one number in unsigned binary, another number in 2's complement, and yet a third in signed magnitude. In addition, it represents something completely different if it were a 10 bit value.
First, let's do the conversion for 8 bit, unsigned binary:
101001102 = 27 + 25 + 22 + 21
101001102 = 128 + 32 + 4 + 2
101001102 = 166
Now let's do the conversion in 2's complement. Before we do, however, let's see how we will do it. First, if the MSB is equal to 1 (which it is in this case), then the value is a negative number. Therefore, we must remove the negative sign before we do the conversion. How do we do this? We take the 2's complement. Once the number is a positive number, then we convert it just like we would a normal unsigned binary value. The flow chart below shows the process graphically.
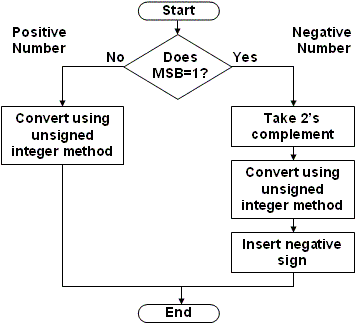
In the case of 101001102, the MSB is a 1. Therefore, it is a negative number, and we must take the two's complement to find the positive counterpart for our negative number.
| Negative value | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1's comp. of negative value | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 2's comp. of negative value | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Now that we have the positive counterpart for the 2's complement value of the negative number 101001102, we convert it to decimal just as we did with the unsigned value.
010110102 = 26 + 24 + 23 + 21
010110102 = 64 + 16 + 8 + 2
010110102 = 90
Since we determined that the 2's complement value was a negative number to begin with, the value of 101001102 in 8 bit, 2's complement form is -90.
Next, let's do the conversion for 8-bit signed magnitude. As with the 2's complement form, the MSB is a 1, therefore, the number is a negative number. The difference is that instead of having to take the 2's complement of the binary value to determine the unsigned value, for signed magnitude we only need to remove the first bit, i.e., the sign bit.
| Meaning of bit position | sign | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Binary value | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
Next, calculate the magnitude just as we would for the unsigned case.
001001102 = 25 + 22 + 21
001001102 = 32 + 4 + 2
001001102 = 38
Since we determined that the signed magnitude value was a negative number to begin with, the value of 101001102 in 8 bit, signed magnitude form is -38.
But what if this number is a 10 bit number and not an 8 bit number? Well, if it's a 10 bit number (00101001102), the MSB is 0 and therefore it is a positive number. Important: The method for converting a positive binary value to a decimal value is the same for all three representations!. Conversion goes something like this:
| Meaning of bit position | MSB | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| Binary value | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
00101001102 = 27 + 25 + 22 + 21
00101001102 = 128 + 32 + 4 + 2
00101001102 = 166
One binary value, 101001102, with four possible ways of interpreting its decimal value. It all depends on how it is represented, 8-bit unsigned, 8-bit signed magnitude, 8-bit 2's complement, or 10 bit.
When using a finite number of bit positions to store information, it is vital to be able to determine the minimum and maximum values that each binary representation can handle. Failure to do this might result in bugs in the programs you create. The following sections calculate the minimum and maximum values possible with each of the three representations using a fixed number of bits, n.
The smallest value representable with unsigned binary representation occurs when all the bits equal zero. Conversion from binary to decimal results in 0 + 0 + ... + 0 = 0. Therefore, for an n bit number:
Minimum unsigned value = 0
The largest value representable with unsigned binary representation occurs when all the bits equal one. Conversion from binary to decimal results in 2n-1 + 2n-2 + ... + 20. Adding one to this equation results in 2n, therefore, for an n bit number:
Maximum unsigned value = 2n - 1
Unlike the unsigned case, the lowest, 2's complement value representable with n bits is not obvious. Remember, 2's complement uses the MSB as a sign bit, and since the lowest value will be negative, the first assumption is to set MSB = 1 (a negative value) and set all the bits after it to one. This should be a really big negative number, right? Well, converting it to decimal results in something like the 8 bit example below:
| 2's comp. value | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Intermediate 1's complement | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Positive value of 2's comp. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Therefore, the decimal equivalent of the 2's complement value of all one's is -1. This isn't the lowest value representable with 2's complement.
It turns out that the lowest possible 2's complement value is an MSB of 1 followed by all zeros as shown in the 8 bit example below. (Remember to follow the flowchart presented in the previous section of this set of notes to convert a negative 2's complement value to decimal.)
| 2's comp. value | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Intermediate 1's complement | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Positive value of 2's comp. | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
If we were to convert this value to decimal using the unsigned method, the result would be -128 for the lowest 8-bit value which is -27. Therefore, for n bits:
Minimum 2's complement value = -2n-1
The maximum value is a little easier to come up with. It is a positive number, i.e., an MSB of 0, with all the magnitude bits set to 1. This would result in a decimal value of 2n-2 + 2n-3 + ... + 20. Therefore, for n bits:
Maximum 2's complement value = 2n-1 - 1
When determining the magnitude of a signed magnitude value, the MSB is thrown away giving you n-1 bits to convert to decimal as if they were unsigned. Therefore, with an MSB representing the sign, the magnitude of the value can reach a maximum of 2n-1-1.
Minimum signed magnitude value = -(2n-1 - 1)
Maximum signed magnitude value = 2n-1 - 1
As an example, the following table compares the minimum and maximum values of an 8 bit number for each of the binary representations.
| Representation | Minimum | Maximum | Total possible values |
| Unsigned | 0 | 255 | 256 |
| 2's Complement | -128 | 127 | 256 |
| Signed Magnitude | -127 | 127 | 255 |
So why does signed magnitude have only 255 possible values that it can represent? It's because 00000000 and 10000000 both represent the same number, a decimal 0.
For decimal numbers with decimal points, the standard way to represent the digits to the right of the decimal point is to continue the powers of ten in decending order starting with -1 where 10-1=1/10th = 0.1. That means that the number 6.5342 has 5 increments of 10-1 (tenths), 3 increments of 10-2 (hundredths), 4 increments of 10-3 (thousandths), and 2 increments of 10-4 (ten-thousandths). The table below shows this graphically.
Exponent |
3 |
2 |
1 |
0 |
-1 |
-2 |
-3 |
-4 |
-5 |
Position value |
1000 |
100 |
10 |
1 |
0.1 |
0.01 |
0.001 |
0.0001 |
0.00001 |
Example |
0 |
0 |
0 |
6 |
5 |
3 |
4 |
2 |
0 |
Therefore, our example has the decimal value 6*1 + 5*0.1 + 3*0.01 + 4*0.001 + 2*0.0001 = 6.5342.
Binary representation with decimal values works the same way except that the position values are powers of two, not powers of ten. So if we needed to convert 10.01101, we could use the same method.
Exponent |
3 |
2 |
1 |
0 |
-1 |
-2 |
-3 |
-4 |
-5 |
Position value |
8 |
4 |
2 |
1 |
0.5 |
0.25 |
0.125 |
0.0625 |
0.03125 |
Decimal |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
Therefore, our example has the decimal value 0*8 + 0*4 + 1*2 + 0*1 +0*0.5 + 1*0.25 + 1*0.125 + 0*0.0625 + 1*0.03125 = 2.40625. In other words, the method of conversion works the same way that it did for the integer values; we've simply added negative powers of two.
Scientific notation, however, is a bit more complex. For example, the number 6.5342 x 10-5 means that we have a decimal value of 0.000065342.
<got here>
The last binary representation (as far as decimal to binary conversions are concerned) is a method to represent floating point numbers. Most floating-point numbers are represented in the computer as a decimal value with an exponent. For example, in scientific notation, we might see the value 0.34237 x 108. This would be a decimal component or mantissa (0.34237) with an exponent 8. A sign bit can also be added. For single-precision, floating point values, the most common method of representation is a 32 bit number organized into the bit representation shown below:
| sign (1 bit) | Exponent, E (8 bit) | Fraction, F (23 bit) |
There are two special cases for this representation: the floating point 0.0 is represented by all bits equaling zero and infinite is represented with the fraction equal to zeros and the exponent equal to all ones.
Otherwise, conversion between floating-point decimal and binary is quite straightforward. First, except for the special case of 0.0, all floating-point numbers have at least one '1' in their magnitude. Therefore, the most significant 1 is assumed and not represented in the fraction. For example, if the 23 bits of the fraction were equal to 01101100101000100000000, the actual binary magnitude of the number would be 1.01101100101000100000000, a 24 bit number determined by adding a binary 1 and a decimal to the MSB position of the 23 bits.
The exponent, E, is applied as a power of two in order to move the decimal place left or right in the binary fraction/magnitude. It is an unsigned number from which is subtracted the value 127. For example, if the exponent, E, of a single-precision, binary, floating-point value were 10001011 (a decimal 139), the actual power of 2 represented by E would be 2(139-127) = 211. Therefore, the decimal point after the assumed 1 of the fraction would be moved 11 positions to the right.
The sign bit simply represents a negative number if it is equal to 1 and a positive number if it is equal to 0.
Let's continue by doing an integer example. How can we represent the decimal integer 23,194 in single-precision, floating-point representation? First, this is a positive number, therefore the sign bit is 0. Next, convert 23,194 to binary.
23,19410 = 1011010100110102
From this, we can get the fraction by moving the implied decimal point 14 positions to the left:
23,19410 = 1.011010100110102 x 214
Since the MSB is always assumed to be 1, the fraction is 01101010011010000000000 (nine zeros added to the right to make it 23 bits). The exponent, E, must satisfy the equation:
14 = E - 127
Therefore, E = 127 + 14 = 141. Converting this to binary gives us E = 100011012. Finally, this gives us the floating-point representation:
23,19410 = 0 10001101 01101010011010000000000
1 0 0 0 0 0 0 0 |
+ 1 0 0 0 1 0 0 1 |
1 0 0 0 1 0 0 1 |
Copyright 2001 by David L. Tarnoff. All rights reserved.